알고리즘 - 순열(Permutation Algorithm)

수학에서 순열(Permutation)또는 치환은 순서가 부여된 임의의 집합을 다른 순서로 뒤섞는 연산이다.

n개의 숫자가 쓰여진 공증에서 r개의 수를 뽑아 나열한 경우의 수.

순서대로 나열한것 = "순열"

 

공식 (nPr)

    서로 다른 n개 중 r개를 선택하는 경우의 수.      (! = 팩토리얼)

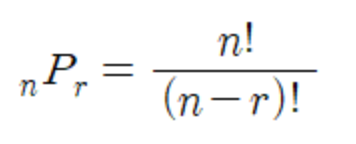
 3P2인 경우 공식은 3! / 1! 가 되므로 3!는 1, 2, 3 = 6이 된다(6개의 경우의 수)

 

모든 경우의 수를 계산하는 완전탐색에서 사용하는 알고리즘이다.

예를들어 {1, 2, 3}이 있다고 했을때 가능한 경우의 수)

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

 

구현방법 -

머리속으로 생각하기 쉽지만 구현은 어렵다.

DFS와 체크리스트를 사용하는게  가장 쉬운 방법.

코드를 외우고 있는것이 좋다.

let input = "123"

func solution(_ numbers:String) -> [Any] {
    let list = numbers.map{ String($0) }
    var checklist = Array(repeating: 0, count: list.count)
    var number = ""
    var result = [Any]()
    
    func DFS(Depth: Int, R: Int, string: String){
        //종료조건
        if( Depth == R){
            //조합된 수를 결과 배열에 추가
            result.append(string)

        }else{
            //0번부터 접근하면서
            for i in 0..<list.count{
                if checklist[i] == 0{ //사용되지 않은 수가있다면
                    number += list[i]  //number에 수를 추가하고
                    checklist[i] = 1   //checklist에 사용했다고 남김.
                    DFS(Depth: Depth + 1, R: R, string: number) //재귀호출 하는데 하나의 수를 선택했으니 Depth1증가
                    checklist[i] = 0 //재귀호출 종료 후 checklist에서 체크 해제
                    number = string //number를 string으로 초기화,
                                    //초기화 하다보면 맨 처음 호출한 string =""가 되어 blank로 남게됨
                }
            }
        }
        
    }
    
    DFS(Depth: 0, R: 2, string: "")
    return result
}