프로그래머스 - 연속 부분 수열 합의 개수[Swift]

연속 부분 수열 합의 개수

문제 설명

철호는 수열을 가지고 놀기 좋아합니다. 어느 날 철호는 어떤 자연수로 이루어진 원형 수열의 연속하는 부분 수열의 합으로 만들 수 있는 수가 모두 몇 가지인지 알아보고 싶어졌습니다. 원형 수열이란 일반적인 수열에서 처음과 끝이 연결된 형태의 수열을 말합니다. 예를 들어 수열 [7, 9, 1, 1, 4] 로 원형 수열을 만들면 다음과 같습니다.

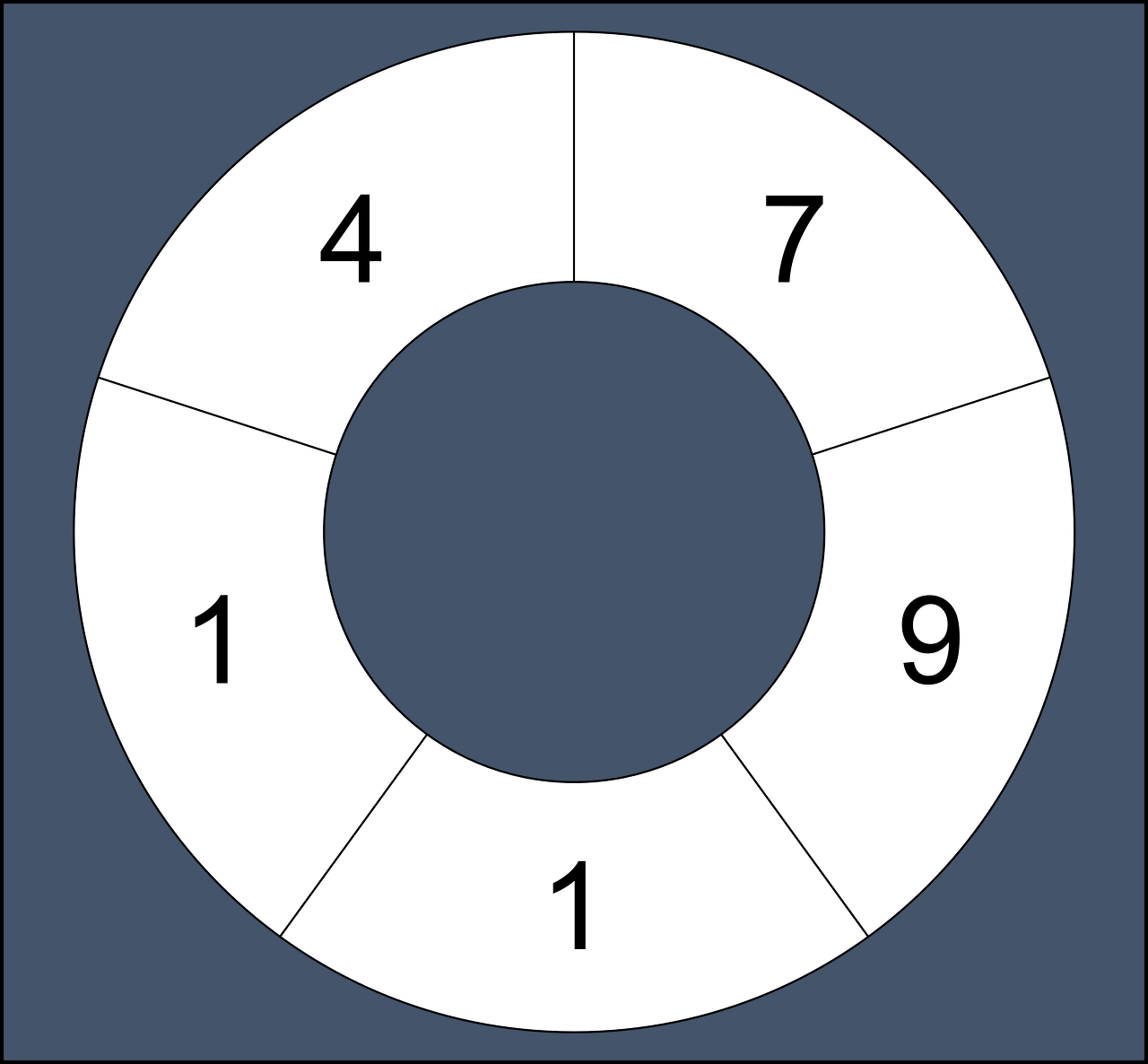
원형 수열은 처음과 끝이 연결되어 끊기는 부분이 없기 때문에 연속하는 부분 수열도 일반적인 수열보다 많아집니다.
원형 수열의 모든 원소 elements가 순서대로 주어질 때, 원형 수열의 연속 부분 수열 합으로 만들 수 있는 수의 개수를 return 하도록 solution 함수를 완성해주세요.

---

제한사항

• 3 ≤ elements의 길이 ≤ 1,000
• 1 ≤ elements의 원소 ≤ 1,000

---

입출력 예elementsresult

[7,9,1,1,4]

18

---

입출력 예 설명

입출력 예 #1
길이가 1인 연속 부분 수열로부터 [1, 4, 7, 9] 네 가지의 합이 나올 수 있습니다.
길이가 2인 연속 부분 수열로부터 [2, 5, 10, 11, 16] 다섯 가지의 합이 나올 수 있습니다.
길이가 3인 연속 부분 수열로부터 [6, 11, 12, 17, 20] 다섯 가지의 합이 나올 수 있습니다.
길이가 4인 연속 부분 수열로부터 [13, 15, 18, 21] 네 가지의 합이 나올 수 있습니다.
길이가 5인 연속 부분 수열로부터 [22] 한 가지의 합이 나올 수 있습니다.
이들 중 중복되는 값을 제외하면 다음과 같은 18가지의 수들을 얻습니다.
[1, 2, 4, 5, 6, 7, 9, 10, 11, 12, 13, 15, 16, 17, 18, 20, 21, 22]

---

풀이 및 소스코드

처음엔 시작인덱스에 개수를 더해 reduce로 합을 구한 후 Set<Int>에 추가하였지만 시간초과가 뜬다.

다른 언어들은 다 위와 같은 방법으로 하던데..?

실패[시간초과]

import Foundation

func solution(_ elements:[Int]) -> Int {
    var result = Set<Int>()
    let long = elements + elements
    
    for many in 0..<elements.count{
        var num = 0
        for idx in 0..<elements.count{
        	//이 reduce부분에서 시간초과
            result.insert(long[idx...idx+many].reduce(0){$0 + $1})
        }
        num = 0
    }
    return result.count
}

그래서 생각한 방법은 누적합이다.

요소가 [1, 2, 3] 3개라고 가정할 경우

1, 2, 3

1 + 2 = 3, 1 + 3, =4

2 + 3 = 5, 2 + 1 = 3

3 + 1 = 4, 3 + 2 = 5

1 + 2 + 3 = 6

1, 2, 3, 3, 4, 5, 3, 4, 5, 6

공백제거 -> 1, 2, 3, 4, 5, 6

8회의 많고 반복된 "+"연산이 필요하다.

누적합으로 할 경우 범위에 대한 reduce과정이 필요없다

1 + 2 = 3 -> 3 + 1 = 4

2 + 3 = 5 -> 5 + 1 = 6

3 + 1 = 4 -> 4 + 2 = 6

6회의 + 연산으로 모든 경우의 수를 구할 수 있다.

 

성공코드

import Foundation

func solution(_ elements:[Int]) -> Int {
    //중복을 제거해야 하므로 Set<Int>를 사용
    var result = Set<Int>()
    //연속된 수열 %처리 해줘도 되지만 2배로 늘려줘도 된다.
    let long = elements + elements
    
    //시작 인덱스부터 원소의 개수만큼 누적되는 누적합을 result에 쌓아간다.
    for idx in 0..<elements.count{
        var num = 0
        for offset in 0..<elements.count{
            num += long[idx+offset]
            result.insert(num)
        }
        num = 0
    }
    return result.count
}

//(0...4)