알고리즘 - 집합 커버 문제(Set Cover)

집합 F에서 선택하는 집합들의 수를 최소화하는 문제

 

신도시를 계획하는데 있어서 학교 배치의 예)

  10개의 마을이 신도시에 만들어질 계획이다.

조건이 만족되어야 한다.

  조건 1. 학교는 마을에 위치해야 한다.

  조건 2. 등교 거리는 걸어서 15분 이내이어야 한다.

2번 마을에 학교를 만들면 1, 2, 3, 4 ,5 마을이 커버된다.

6번 마을에 학교를 만들면 5, 6, 7, 9, 19 마을이 커버된다.

 

최소 학교의 수 = 2개

 

전체 마을의 수

U = {1, 2,3 ,4, 5, 6, 7, 8, 9 ,19}

 

한 마을에 배치했을때 커버되는 마을의 집합

S1 = {1, 2, 3, 8}

S2 = {1, 2, 3, 4, 8}

S3 = {1, 2, 3, 4}

S4 = {2, 3, 4, 5, 7, 8}

S5 = {4, 5, 6, 7}

S6 = {5, 6 , 7, 9, 10}

S7 = {4, 5, 6, 7}

S8 = {1, 2, 4, 8}

S9 = {6, 9}

S10 = {6, 10}

 

집합들중 어떤 마을을 선택해야 그들의 합집합이 U와 같은가

S2 U S6 = U

 

단순한 해결 방법

F에 n개의 집합이 있다고 가정한다.

F에 있는 집합의 모든 조합을 1개씩 합집합 해보고 U가 되는지 확인한다.

U가 되는 조합의 집합 수가 최소인 것을 찾는다.

 

n개의 집합이 있을 경우 2^n - 1개를 검사해야 한다.

n이 커지면 최적해를 찾는 것은 실질적으로 불가능해진다.

이를 극복하기 위한 방법으로 최적해를 찾는 대신에 근접한 근사해(Approximation solution)를 찾는다.

 

수행과정

C = {}

U = {1, 2,3 ,4, 5, 6, 7, 8, 9 ,19}

 

F = {S1, S2, S3, S4, S5, S6, S7, S8, S9, S10}

S1 = {1, 2, 3, 8}

S2 = {1, 2, 3, 4, 8}

S3 = {1, 2, 3, 4}

S4 = {2, 3, 4, 5, 7, 8}

S5 = {4, 5, 6, 7}

S6 = {5, 6 , 7, 9, 10}

S7 = {4, 5, 6, 7}

S8 = {1, 2, 4, 8}

S9 = {6, 9}

S10 = {6, 10}

 

U의 원소를 가장 많이 커버하는 집합을 찾는다 -> S4

 

U에서 S4요소를 뺀다.

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - {2, 3, 4, 5, 7, 8}

U = {1, 6, 9, 10}

 

F에서 S4를 뺀다.

F = {S1, S2, S3, S5, S6, S7, S8, S9, S10}

 

C에 S4를 추가

C = {S4}

 

U = {1, 6, 9, 10}을 가장 많이 커버하는 집합을 찾는다.

S6 = {5, 6, 7, 9, 10}을 선택

 

U에서 S6를 뺀다.

{1,  6, 9, 10} - {5, 6, 7, 9, 10}

U = {1}

 

S6에서 F를 제거하고 S6를 C에 추가

F = {S1, S2, S3, S5, S7, S8, S9, S10}

C = {S4, S6}

 

U = {1}을 가장 많이 커버하는 집합을 선택하고 뺀다

U = U - S1{1, 2, 3, 8}

U = {}

 

S1을 F에서 제거하고 C에 추가

F = {S2, S3, S5, S7, S8, S9, S10}

C = {S1, S4, S6}

 

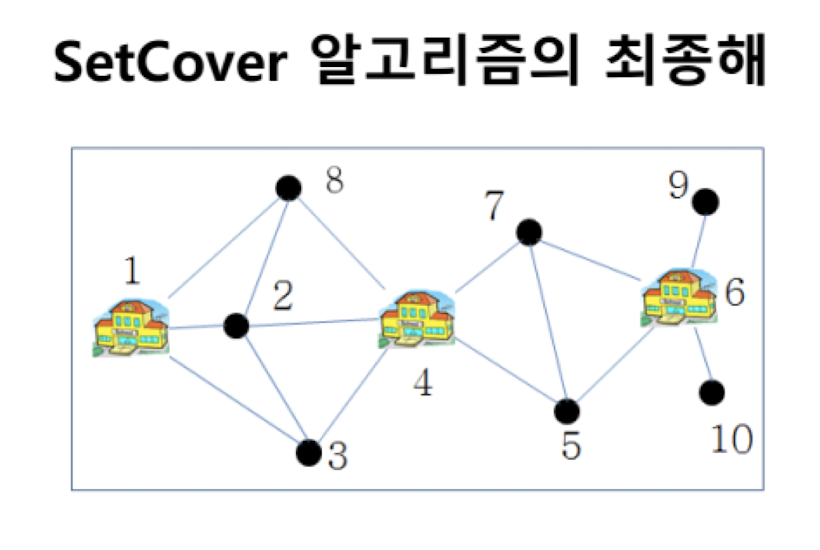
결과 C = {S1, S4, S6}

SetCover 알고리즘의 최종해가 된다.

 

시간 복잡도

O(n^3)