작업의 수행 시간이 중복되지 않도록 모든 작업을 가장 적은 수의 기계에 배정하는 문제
대학 수업에서 강의실을 배정하는 문제와 같다.
강의실 = "기계"
강의 = "작업"
주어진 요소
- 작업의 수
- 각 작업의 시작시간과 종료시간
- 작업의 길이
알고리즘
다음과 같은 그리디 알고리즘이 존재한다.
- 빠른 시작시간 작업 우선(Earliest start time first)배정
- 빠른 종료시간 작업 우선(Earliest finish time first)배정
- 짧은 작업 우선(Shortest job first)배정
- 긴 작업 우선(Longest job first)배정
위 4가지중 첫 번째 알고리즘을 제외하고 나머지 3가지는 항상 최적해를 찾지 못한다.
빠른 시작시간 작업 우선(Earliest start time first)배정 알고리즘
예제)
t = [s, f]
s는 시작시간, f는 종료시간
t1 = [7, 8]
t2 = [3, 7]
t3 = [1, 5]
t4 = [5, 9]
t5 = [0, 2]
t6 = [6, 8]
t7 = [1, 6]
시작시간을 오름차순으로 정렬한다.
L = {[0, 2], [1, 6], [1, 5], [3, 7], [5, 9], [6, 8], [7, 8]}
시작시간에 따라 정렬된 순서대로 배정을 하는데, 먼저 생성된 기계 순서대로 t가 배치될 수 있는지 확인하고, 배치될 수 있는 기계가 없을 때 기계를 생성한다.
L = {[1, 6], [1, 5], [3, 7], [5, 9], [6, 8], [7, 8]}

L = {[1, 5], [3, 7], [5, 9], [6, 8], [7, 8]}
다음 순서인 [1, 6]이 배치될 수 있는 Machine이 없으므로 생성.
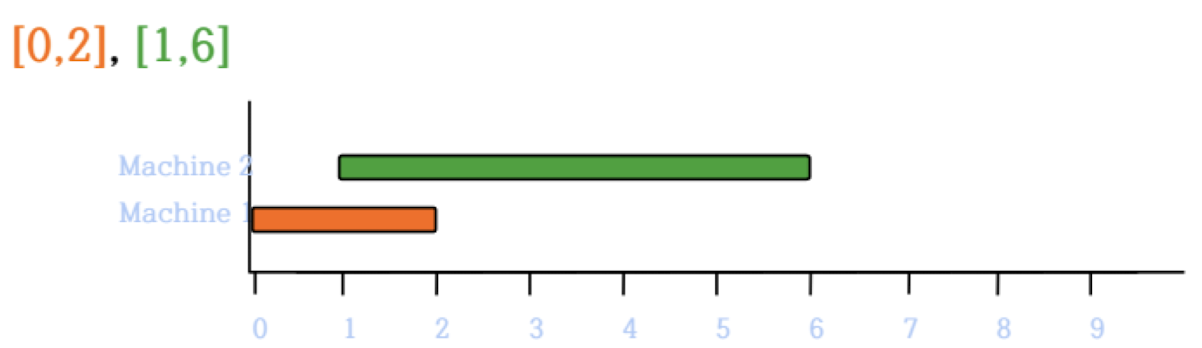
L = {[3, 7], [5, 9], [6, 8], [7, 8]}
Machine 생성
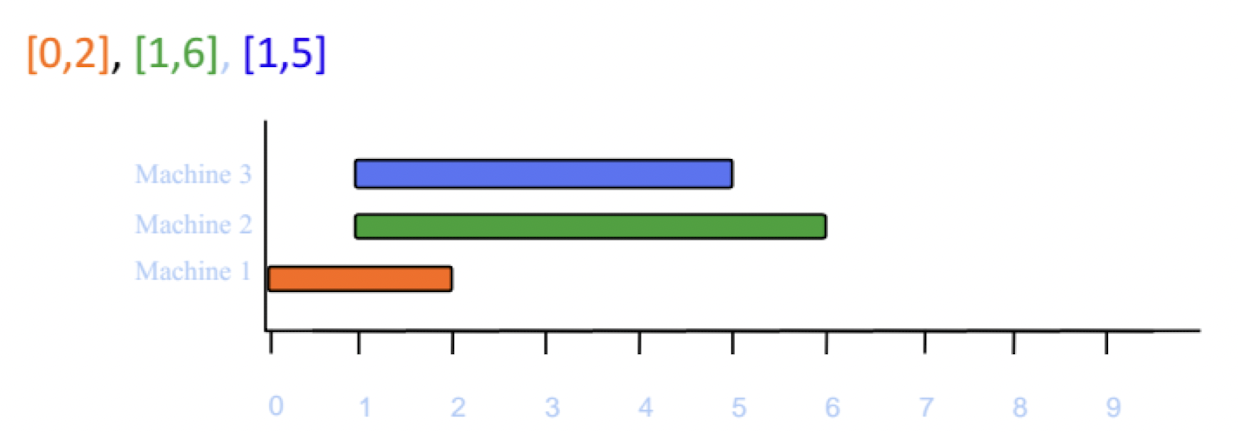
L = {[5, 9], [6, 8], [7, 8]}
[3, 7]은 Machine1에 들어갈 수 있다.
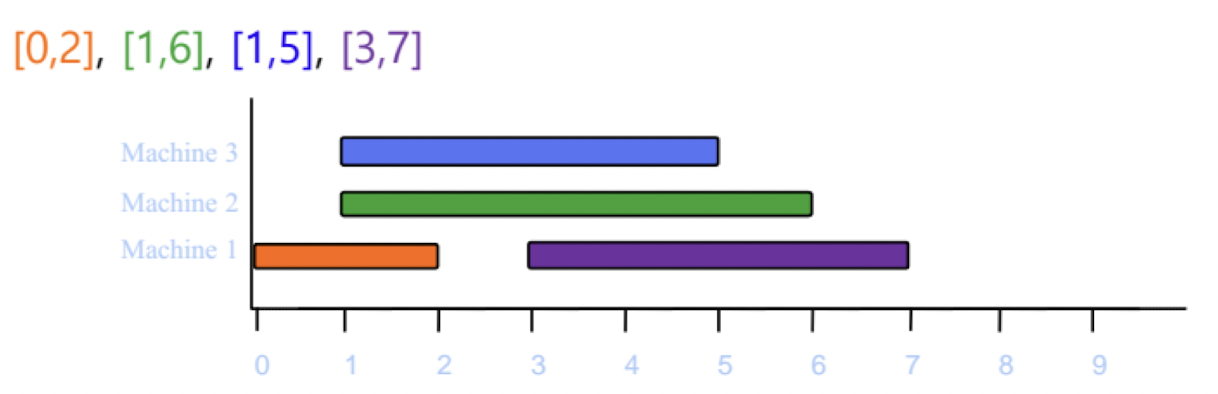
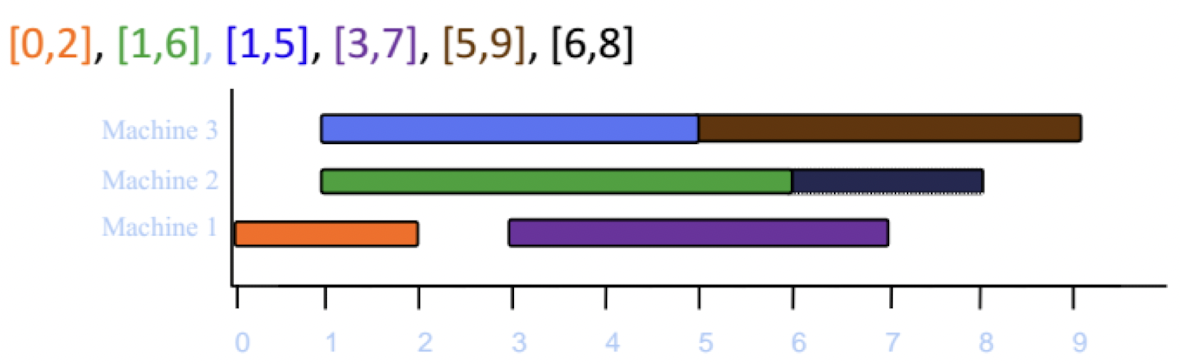
L = {[6, 8], [7, 8]}
[5, 9]는 Machine3에 들어갈 수 있다.
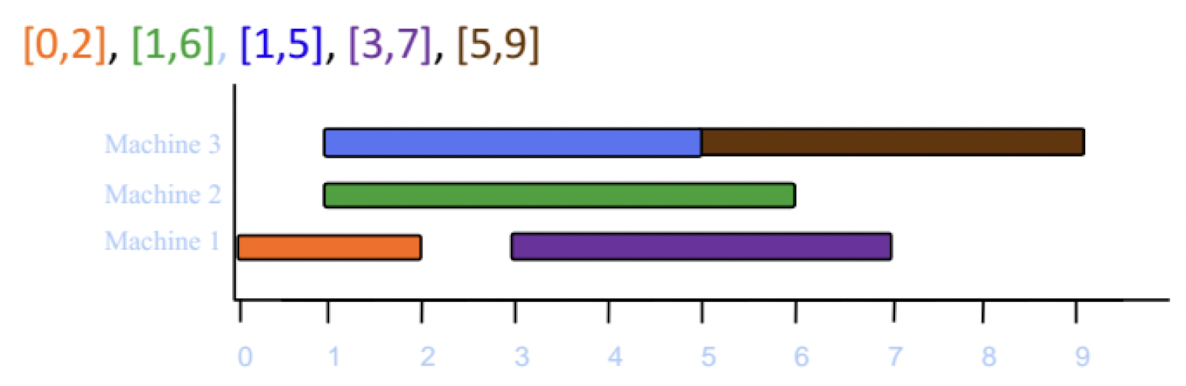
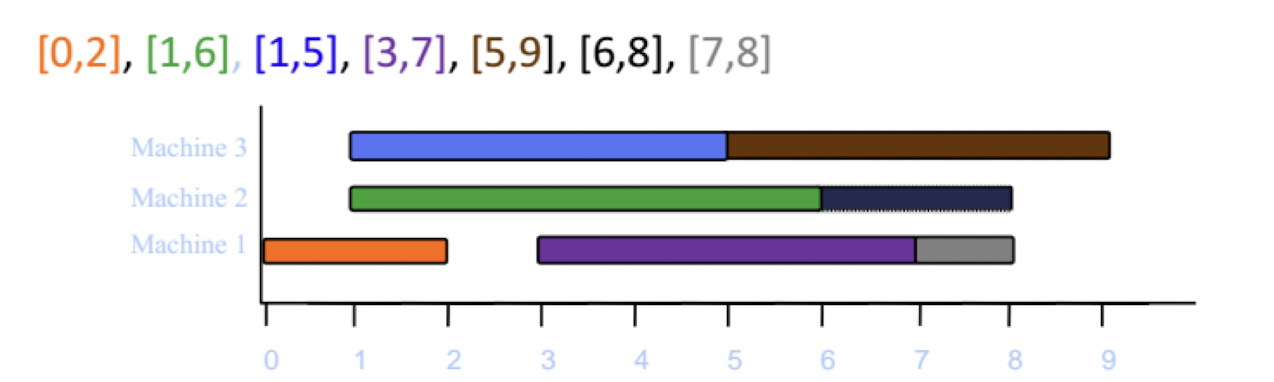
L = {[7, 8]}
L = {}
시간복잡도
m = 사용된 기계의 수
n = 작업의 개수
O(n log n) + O(mn)
